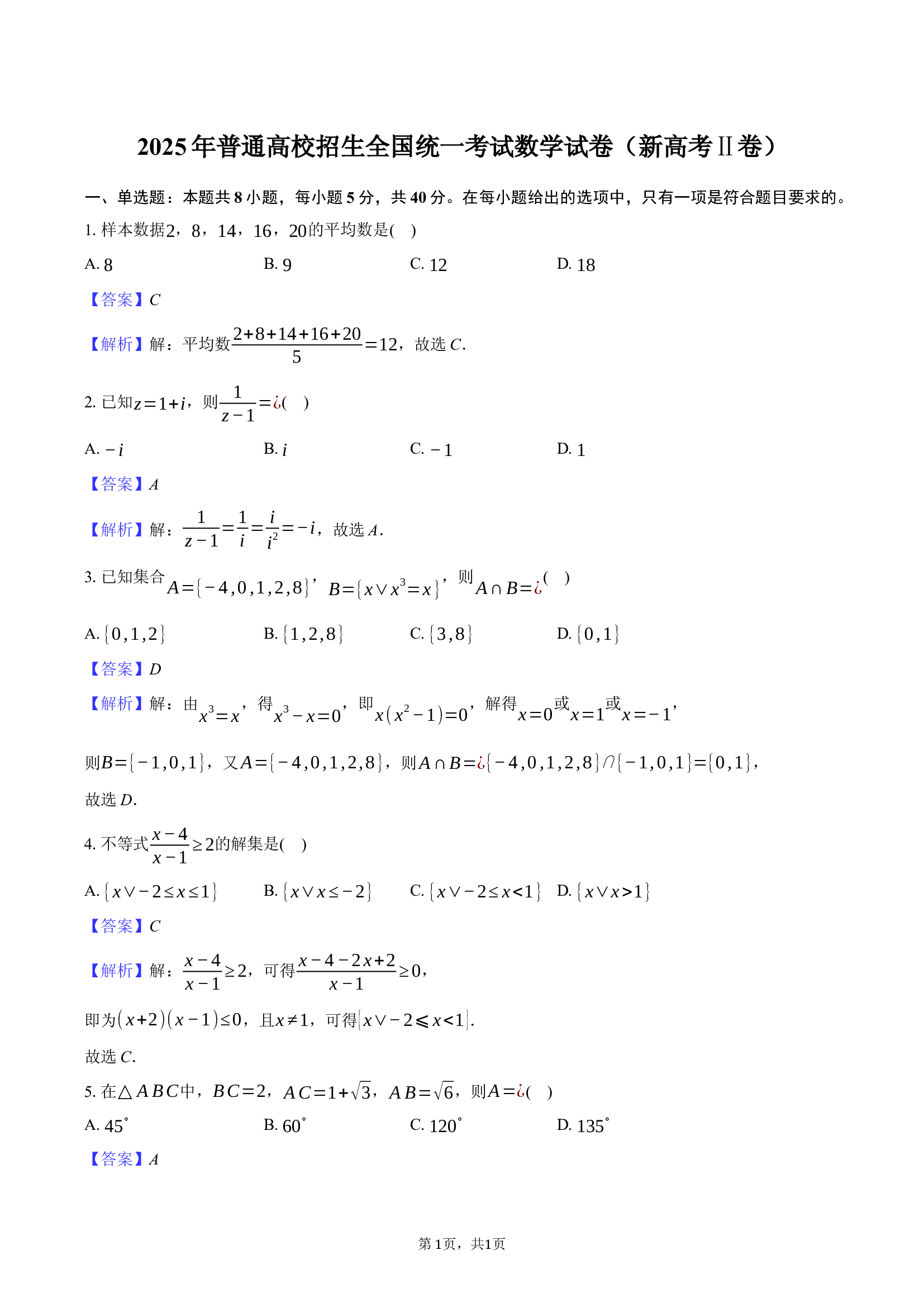
2025年普通高校招生全国统一考试数学试卷（新高考Ⅱ卷）-教师版.docx

2025 年普通高校招生全国统一考试数学试卷（新高考 Ⅱ 卷） 一、单选题：本题共 8 小题，每小题 5 分，共 40 分。在每小题给出的选项中，只有一项是符合题目要求的。 1 . 样本数据 ， ， ， ， 的平均数是 (    ) A. B. C. D. 【答案】 C   【解析】 解：平均数 ，故选 C ． 2 . 已知 ，则 (    ) A. B. C. D. 【答案】 A   【解析】 解： ，故选 A ． 3 . 已知集合 ， ，则 (    ) A. B. C. D. 【答案】 D   【解析】 解：由 ，得 ，即 ，解得 或 或 ， 则 ，又 ，则 ， 故选 D ． 4 . 不等式 的解集是 (    ) A. B. C. D. 【答案】 C   【解析】 解： ，可得 ， 即为 ，且 ，可得 ． 故选 C ． 5 . 在 中， ， ， ， 则 (    ) A. B. C. D. 【答案】 A   【解析】 解： ， 又 中 ，所以 ， 故选： ． 6 . 设抛物线 的焦点为 ， 在 上，过 作 准线的垂线，垂足为 ，若直线 的方程为 ，则 (    ) A. B. C. D. 【答案】 C   【解析】 解：抛物线的焦点 ，准线 ， 设 ，则 ， 将 坐标代入直线 ，得 ， 直线 斜率 ，解得 ， 由 在抛物线上，有 ，将 代入得 ， 由抛物线定义， ． 故选 C ． 7 . 记 为等差数列 的前 项和，若 ， ，则 (    ) A. B. C. D. 【答案】 B   【解析】 解：由已知条件可知， 和 ， 可列出以下方程组： ， 解得： ， 根据等差数列前 项和的公式 ， 可得 ． 故选 B ． 8 . 已知 ， ，则 (    ) A. B. C. D. 【答案】 D   【解析】 解： ， ， ， ， ． 二、多选题：本题共 3 小题，共 18 分。在每小题给出的选项中，有多项符合题目要求。 9 . 记 为等比数列 的前 项和， 为 的公比，且 ，若 ， ，则 (    ) A. B. C. D. 【答案】 AD   【解析】 解：已知 所以 将 带入得： 化简得： 因为 ，解得 舍去负根 ，故 A 正确； 选项 B ： ；错误； 选项 C ： ； C 错误； 选项 D ： 因此， 正确，故选 AD ． 10 . 已知 是定义在 上奇函数，且当 时， ，则 (    ) A. B. 当 时， C. ，当且仅当 D. 是 极大值点 【答案】 ABD   【解析】 解：选项 A 定义域为 的奇函数在 处的值为 ，因此 ，正确． 选项 B 对于 ，利用奇函数性质 ，代入 的表达式得： ，正确． 选项 C 当 时， 解不等式 ，得 ，当 时， ， 例如 时， ， 说明存在 时 的情况， 因此“当且仅当 错误． 选项 D 当 时， ，求导得 ，令 ，解得 导数在 两侧由正变负，故为极大值点，正确． 故选 ABD ． 11 . 双曲线 的左、右焦点分别是 ， ，