苏教版必修第二册《第十二章复数》
2025
年单元测试卷(
1
)
一、单选题:本题共
14
小题,每小题
5
分,共
70
分。在每小题给出的选项中,只有一项是符合题目要求的。
1
.
在复平面内,复数
的共轭复数对应的点位于
( )
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
2
.
已知
是虚数单位,则复数
的共轭复数的虚部为
( )
A.
B.
C.
D.
3
.
复数
满足
,其中
是虚数单位,则
( )
A.
B.
C.
D.
4
.
已知复数
的实部为正数,虚部为
,
,则
( )
A.
B.
C.
D.
5
.
已知复数
是关于
的方程
的一个根,若复数
满足
,复数
在复平面内对应的点
的集合为图形
,则
得周长为
( )
A.
B.
C.
D.
6
.
已知复数
其中
是虚数单位
的实部与虚部相等,则实数
等于
( )
A.
B.
C.
D.
7
.
设复数
满足
,
在复平面内对应的点为
,则
( )
A.
B.
C.
D.
8
.
若
,则
( )
A.
B.
C.
D.
9
.
设复数
满足
为虚数单位
,则复数
的共轭复数在复平面内对应的点位于
( )
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
10
.
若复数
在复平面内对应的点在第四象限,则实数
的取值范围是
( )
A.
B.
C.
D.
11
.
已知复数
,则
( )
A.
B.
C.
D.
12
.
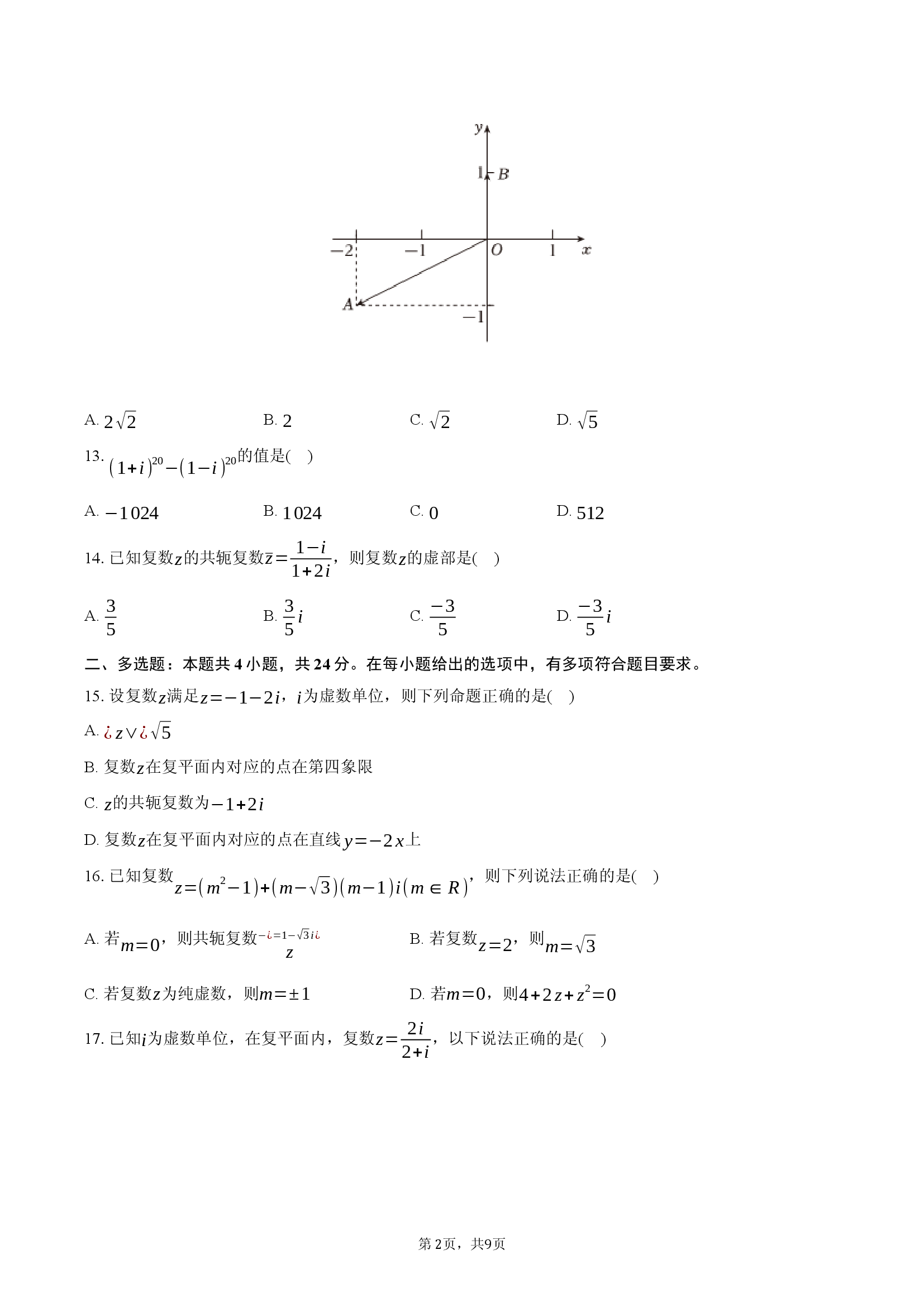
如图,在复平面内,复数
,
对应的向量分别是
,
,则
的值为
( )
A.
B.
C.
D.
13
.
的值是
( )
A.
B.
C.
D.
14
.
已知复数
的共轭复数
,则复数
的虚部是
( )
A.
B.
C.
D.
二、多选题:本题共
4
小题,共
24
分。在每小题给出的选项中,有多项符合题目要求。
15
.
设复数
满足
,
为虚数单位,则下列命题正确的是
( )
A.
B.
复数
在复平面内对应的点在第四象限
C.
的共轭复数为
D.
复数
在复平面内对应的点在直线
上
16
.
已知复数
,则下列说法正确的是
( )
A.
若
,则共轭复数
B.
若复数
,则
C.
若复数
为纯虚数,则
D.
若
,则
17
.
已知
为虚数单位,在复平面内,复数
,以下说法正确的是
( )
A.
复数
的虚部是
B.
C.
复数
的共轭复数是
D.
复数
的共轭复数对应的点位于第四象限
18
.
已知集合
,其中
为虚数单位,则下列元素属于集合
的是
( )
A.
B.
C.
D.
三、填空题:本题共
4
小题,每小题
5
分,共
20
分。
19
.
已知复数
,
,
在复平面上对应的点分别为
,
,
,若四边形
为平行四边形
为复平面的坐标原点
,则复数
______
.
20
.
瑞士数学家欧拉于
年在
微分公式
中,第一次用
来表示
的平方根,首创了用符号
作为虚数的单位.若复数
为虚数单位
,则复数
的虚部为
,
.
21
.
是虚数单位,复数
______
.
22
.
设复数
满足
,则
的取值范围是
.
四、解答题:本题共
3
小题,共
36
分。解答应写出文字说明,证明过程或演算步骤。
23
.
本小题
分
在复平面内,向量
所对的复数
,向量
所对的复数
,
点所对应的复数
,
点与
点关于虚轴对称.
求点
、
、
、
的坐标;
判断
、
、
、
四点是否共圆,并证明你的结论.
24
.
本小题
分
已知
,
,
,
是复平面内的四个点,其中
,
,且向量
,
对应的复数分别为
,
,且
.
求
,
;
若复数
,
,在复平面内对应的点
在第四象限,求实数
的取值范围.
25
.
本小题
分
已知
为三角形的一个内角,复数
,且满足
.
求
;
设
,
,
在复平面上对应的点分别为
,
,
,求
的面积.
答案和解析
1.
【答案】
【解析】
复数
,
则复数
的共轭复数为
,
在复平面内,复数
的共轭复数对应点的坐标为
,
故在复平面内,复数
的共轭复数对应的点位于在第四象限.
故选
D
.
2.
【答案】
【解析】
复数
的共轭复数:
.
它的虚部为
.
故选:
.
3.
【答案】
【解析】
,
.
故选:
.
4.
【答案】
【
解析】
复数
的实部为正数,虚部为
,
则
,
,
则
,解得
,
故
.
故选:
.
5.
【答案...
苏教版必修第二册《第十二章 复数》2025年单元测试卷(1).docx