必刷大题
20
概率与统计
1
.
(
2023·
汕头模拟
)
袋中装着标有数字
1
,
2
,
3
,
4
的小球各
3
个
,
从袋中任取
3
个小球
,
每个小球被取出的可能性都相等
.
(
1
)
求取出的
3
个小球上的数字互不相同的概率
;
(
2
)
用
X
表示取出的
3
个小球上所标的最大数字
,
求随机变量
X
的分布列和数学期望
.
解
(
1
)
“
一次取出的
3
个小球上的数字互不相同
”
的事件记为事件
A
,
则
P
(
A
)
=
=
.
(
2
)
由题意知,
X
所有可能的取值为
1
,
2
,
3
,
4
,
P
(
X
=
1
)
=
=
,
P
(
X
=
2
)
=
=
,
P
(
X
=
3
)
=
=
=
,
P
(
X
=
4
)
=
=
=
.
所以随机变量
X
的分布列为
X
1
2
3
4
P
随机变量
X
的数学期望为
E
(
X
)
=
1
×
+
2
×
+
3
×
+
4
×
=
.
2
.
(
2023·
邵阳模拟
)
某电视台为了解不同性别的观众对同一档电视节目的评价情况
,
随机选取了
100
名观看该档节目的观众对这档电视节目进行评价
,
已知被选取的观众中
“
男性
”
与
“
女性
”
的人数之比为
9
∶
11
,
评价结果分为
“
喜欢
”
和
“
不喜欢
”
,
并将部分评价结果整理如下表所示
.
性别
评价
合计
喜欢
不喜欢
男性
15
女性
合计
50
100
(
1
)
根据所给数据
,
完成上面的
2
×
2
列联表
;
(
2
)
依据小概率值
α
=
0.005
的独立性检验
,
能否认为性别因素与评价结果有关系
?
(
3
)
电视台计划拓展男性观众市场
,
现从参与评价的男性中
,
用按比例分配的分层随机抽样的方法选取
3
人
,
进行节目
“
建言
”
征集奖励活动
,
其中评价结果为
“
不喜欢
”
的观众
“
建言
”
被采用的概率为
,
评价结果为
“
喜欢
”
的观众
“
建言
”
被采用的概率为
,
“
建言
”
被采用奖励
100
元
,
“
建言
”
不被采用奖励
50
元
,
记
3
人获得的总奖金为
X
,
求
X
的分布列及数学期望
.
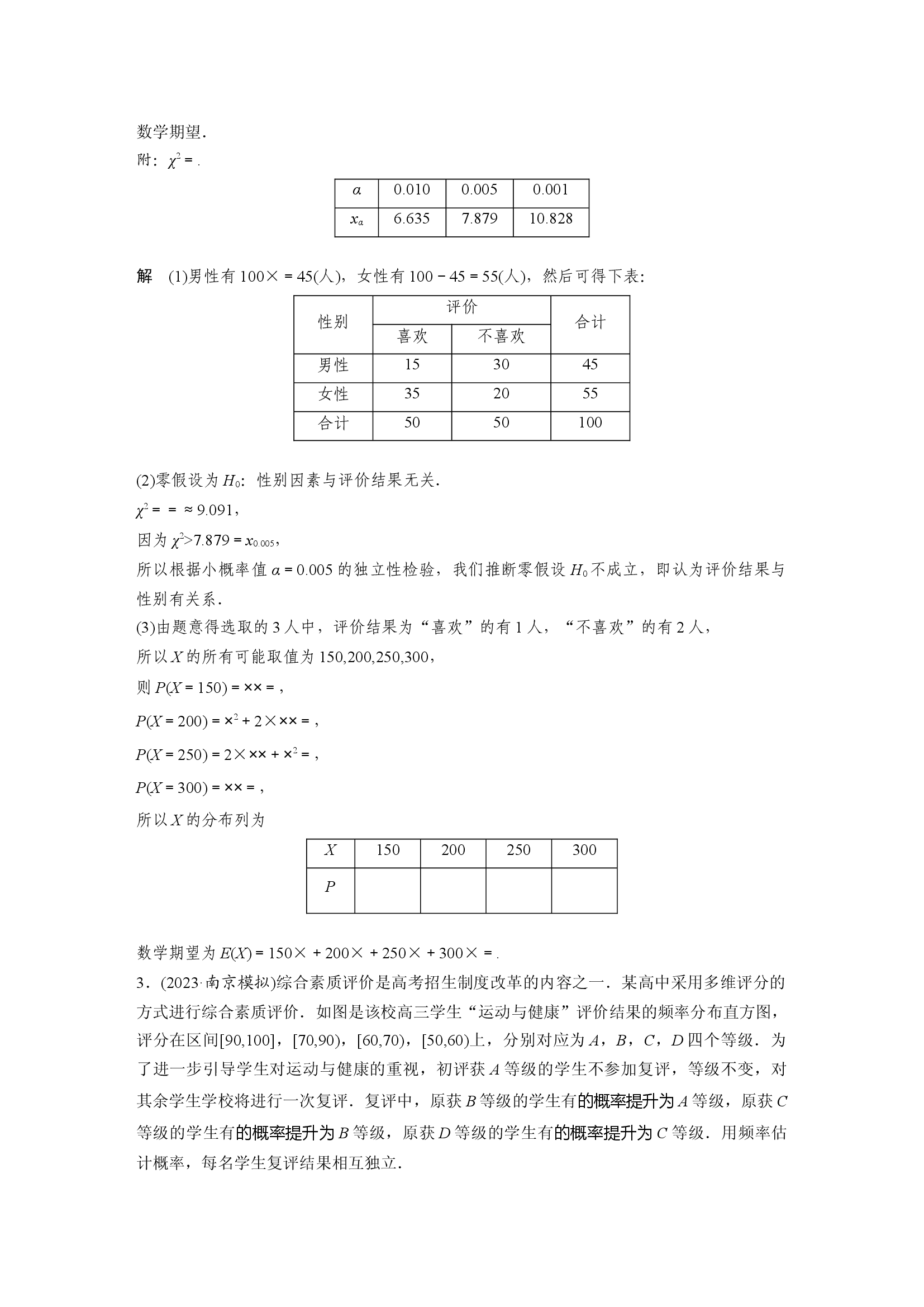
附:
χ
2
=
.
α
0.010
0.005
0.001
x
α
6.635
7.879
10.828
解
(
1
)
男性有
100
×
=
45
(
人
)
,女性有
100
-
45
=
55
(
人
)
,然后可得下表:
性别
评价
合计
喜欢
不喜欢
男性
15
30
45
女性
35
20
55
合计
50
50
100
(
2
)
零假设为
H
0
:性别因素与评价结果无关
.
χ
2
=
=
≈
9.091
,
因为
χ
2
>7.879
=
x
0.005
,
所以根据小概率值
α
=
0.005
的独立性检验,我们推断零假设
H
0
不成立,即认为评价结果与性别有关系
.
(
3
)
由题意得选取的
3
人中,评价结果为
“
喜欢
”
的有
1
人,
“
不喜欢
”
的有
2
人,
所以
X
的所有可能取值为
150
,
200
,
250
,
300
,
则
P
(
X
=
150
)
=
×
×
=
,
P
(
X
=
200
)
=
×
2
+
2
×
×
×
=
,
P
(
X
=
250
)
=
2
×
×
×
+
×
2
=
,
P
(
X
=
300
)
=
×
×
=
,
所以
X
的分布列为
X
150
200
250
300
P
数学期望为
E
(
X
)
=
150
×
+
200
×
+
250
×
+
300
×
=
.
3
.
(
2023·
南京模拟
)
综合素质评价是高考招生制度改革的内容之一
.
某高中采用多维评分的方式进行综合素质评价
.
如图是该校高三学生
“
运动与
健康
”
评价结果的频率分布直方图
,
评分在区间
[
90
,
100
]
,
[
70
,
90
)
,
[
60
,
70
)
,
[
50
,
60
)
上
,
分别对应为
A
,
B
,
C
,
D
四个等级
.
为了进一步引导学生对运动与健康的重视
,
初评获
A
等级的学生不参加复评
,
等级不变
,
对其余学生学校将进行一次复评
.
复评中
,
原获
B
等级的学生有
的概率提升为
A
等级
,
原获
C
等级的学生有
的概率提升为
B
等级
,
原获
D
等级的学生有
的概率提升为
C
等级
.
用频率估计概率
,
每名学生复评结果相互独立
.
(
1
)
若初评中甲获得
B
等级
,
乙
、
丙获得
C
等级
,
记甲
、
乙
、
丙三人复评后等级为
B
等级的人数为
ξ
,
求
ξ
的分布列和数学期望
;...
第十章 必刷大题20 概率与统计.docx