2025
年高三专项训练:空间直角坐标系的构建策略
一、单选题
1
.
正方体
中,
,
分别是
,
的中点,则
与截面
所成的角的正切值为
( )
A.
B.
C.
D.
2
.
在直三棱柱
中,底面是等腰直角三角形,
,侧棱
,
,
分别是
与
的中点,点
在平面
上的射影是
的重心
,则点
到平面
的距离为
( )
A.
B.
C.
D.
3
.
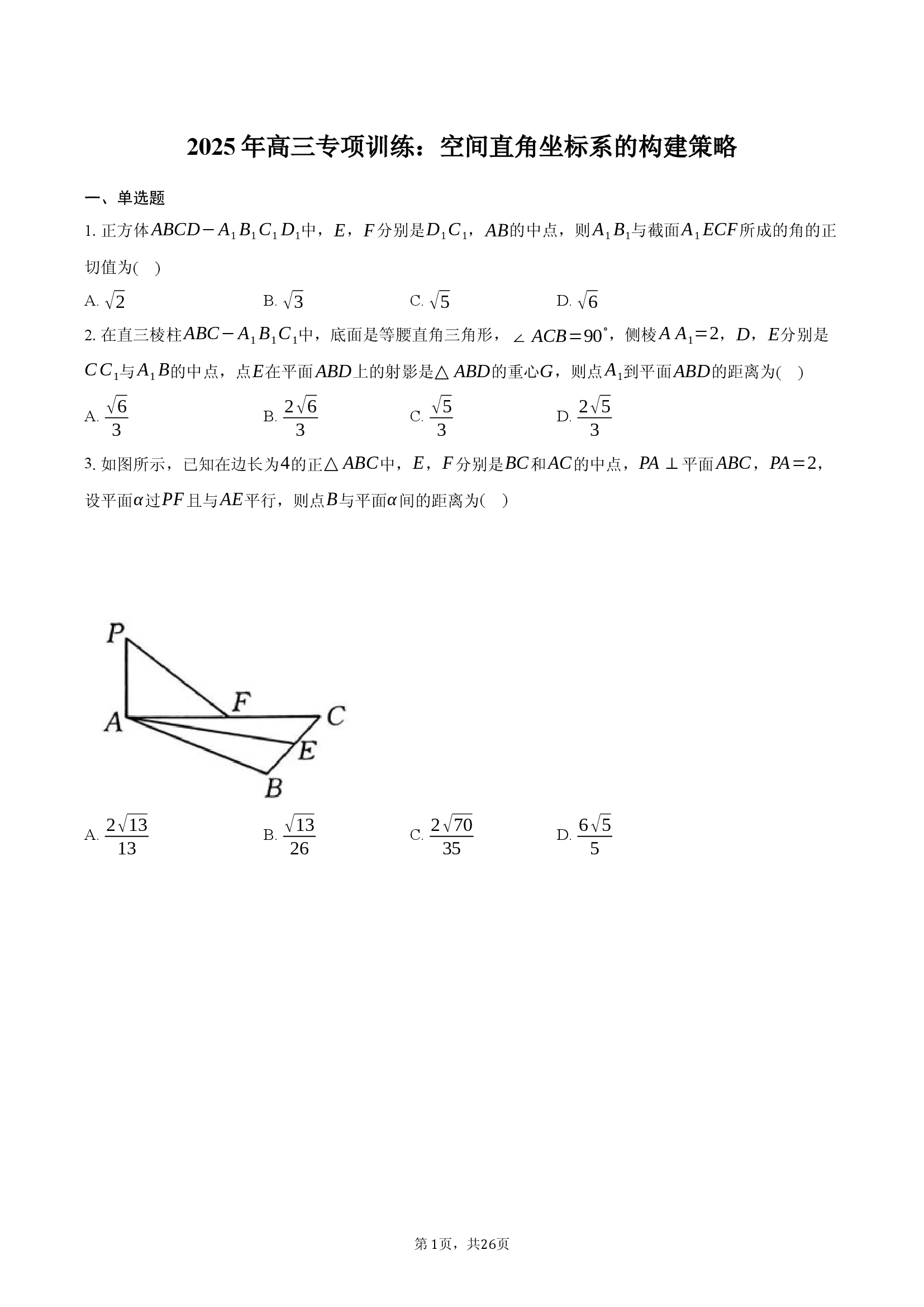
如图所示,已知在边长为
的正
中,
,
分别是
和
的中点,
平面
,
,设平面
过
且与
平行,则点
与平面
间的距离为
( )
A.
B.
C.
D.
4
.
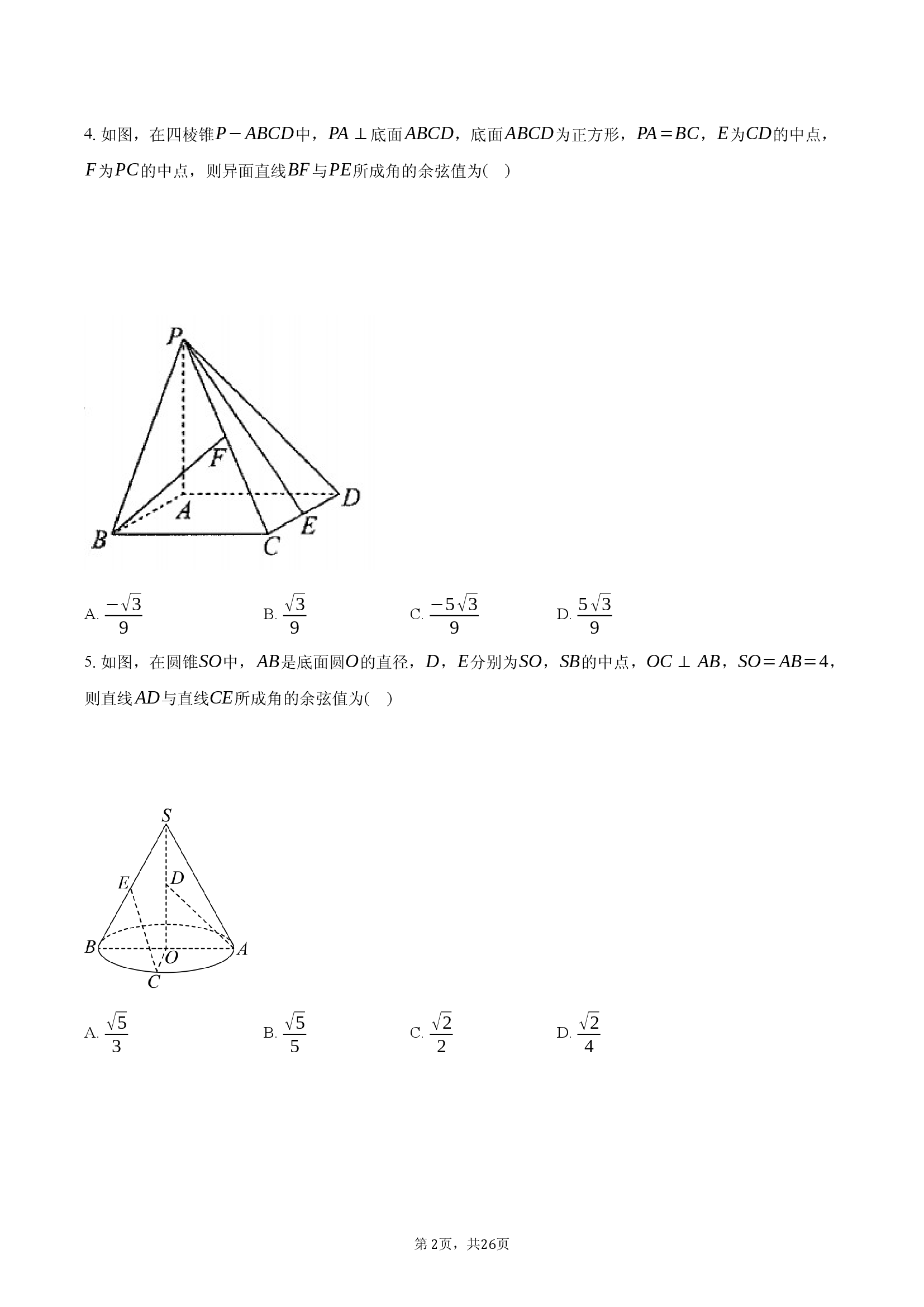
如图,在四棱锥
中,
底面
,底面
为正方形,
,
为
的中点,
为
的中点,则异面直线
与
所成角的余弦值为
( )
A.
B.
C.
D.
5
.
如图,在圆锥
中,
是底面圆
的直径,
,
分别为
,
的中点,
,
,则直线
与直线
所成角的余弦值为
( )
A.
B.
C.
D.
6
.
在直三棱柱
中,已知
,
,
是
的中点,
是
的中点,
是
的中点,则直线
与
所成的角为
( )
A.
B.
C.
D.
7
.
如图所示,在底面是直角梯形的四棱锥
中,侧棱
底面
,
,
,
,
,则点
到平面
的距离为
( )
A.
B.
C.
D.
8
.
如图,
与
都是边长为
的正三角形,平面
平面
,
平面
,
,则点
到平面
的距离为
( )
A.
B.
C.
D.
二、多选题
9
.
如图,在四面体
中,
,
是
的中点,则下列结论正确的是
( )
A.
平面
平面
B.
直线
与直线
所成角为
C.
直线
与平面
所成角的余弦值为
D.
四面体
的外接球表面积为
10
.
如图,菱形
边长为
,点
为边
的中点,将
沿
折起,使点
到点
,连接
,
,且
,平面
与平面
的交线为
,则下列结论中正确的是
( )
A.
平面
平面
B.
C.
三棱锥
外接球的体积为
D.
平面
与平面
的夹角的余弦值为
三、填空题
11
.
在正四棱锥
中,底面边长为
,侧棱
,
为
的中点,
为直线
上一点,且
与
、
不重合,若异面直线
与
所成角为
,则三棱锥
的体积为
.
12
.
在我国古代数学名著
九章算术
中,将四个面都为直角三角形的三棱锥称之为鳖臑
已知在鳖臑
中,
平面
,
,
为
的中点,则点
到平面
的距离为
.
13
.
三菱锥
中,
且
、
、
两两垂直,
是
中点,则直线
与
所成角的余弦值为
14
.
在中国古代数学著作
九章算术
中记载了一种称为“曲池”的几何体,该几何体的上、下底面平行,且均为扇环形
扇环是指圆环被扇形截得的部分
现有一个如图所示的曲池,它的高为
,
,
,
,
均与曲池的底面垂直,底面扇环对应的两个圆的半径分别为
和
,对应的圆心角为
,则图中平面
与平面
所成角的余弦值为
.
15
.
如图,在四棱柱
中,
底面
,且底面
为菱形,
,
,
,
为
的中点,
在
上,
在平面
内运动
不与
重合
,且
平面
,异
面直线
与
所成角的余弦值为
,则
的最大值为
.
16
.
如图,在六面体
中,平面
平面
,四边形
与四边形
是两个全等的矩形,
,
,
平面
,
,
,
,则
.
17
.
九章算术
第五卷中涉及一种几何体
羡除,它下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺.该羡除是一个多面体
,如图,四边形
,
均为等腰梯形,
,平面
平面
,梯形
和梯形
的高分别为
,
,且
,
,
,则
.
18
.
如图,
,
两点都在以
为直径的球
的表面上,
,
,
,若球
的表面积为
,则异面直线
与
所成角的余弦值为
.
19
.
已知斜三棱柱
,它的每条棱长均为
,并且侧面
与底面
垂直,
,则
与底面
所成角的正弦值为
,
.
四、解答题
20
.
如图,
和
所在平面互相垂直,且
,
,
,
分别为
,
的中点
求证:
.
21
.
如图,已知四棱锥
的底面
为菱形,且
平面
,
,
,
,且
,
分别为
,
的中点.
求证:
平面
;
求二面角
的余弦值.
22
.
如图,四棱锥
中,四边形
是平行四边形,点
为线段
的中点.
求证:
平面
;
若四边形
为菱形,且
,
,
,
平面
,求平面
与平面
所成二面角的正弦值.
23
.
如图,在空间几何体
中,平面
平面
,
...
2025年高三专项训练:空间直角坐标系的构建策略.docx