2025
年高三专项训练:圆锥曲线中的探究性问题
一、单选题
1
.
已知曲线
,对于命题:
垂直于
轴的直线与曲线
有且只有一个交点;
若
,
为曲线
上任意两点,则有
下列判断正确的是
.
A.
和
均为真命题
B.
和
均为假命题
C.
为真命题,
为假命题
D.
为假命题,
为真命题
2
.
如图
,某家用电暖器是由反射面、热馈源、防护罩及支架组成,为了更好利用热效能,反射面设计成抛物面
抛物线绕其对称轴旋转形成的曲面
,热馈源安装在抛物线的焦点处,圆柱形防护罩的底面直径等于抛物面口径
图
是该电暖器的轴截面,防护罩的宽度
等于热馈源
到口径
的距离,已知口径长为
,防护罩宽为
,则顶点
到防护罩外端
的距离为
( )
A.
B.
C.
D.
3
.
已知椭圆和双曲线有共同的焦点
,
,
,
分别是它们在第一象限和第三象限的交点,且
,记椭圆和双曲线的离心率分别为
,
,则
等于
( )
A.
B.
C.
D.
4
.
已知点
是椭圆
上一点,
,
分别是圆
和圆
上的点,那么
的最小值为
( )
A.
B.
C.
D.
5
.
已知点
是双曲线
下支上的一点,
、
分别是双曲线的上、下焦点,
是
的内心,且
,则双曲线的离心率为
( )
A.
B.
C.
D.
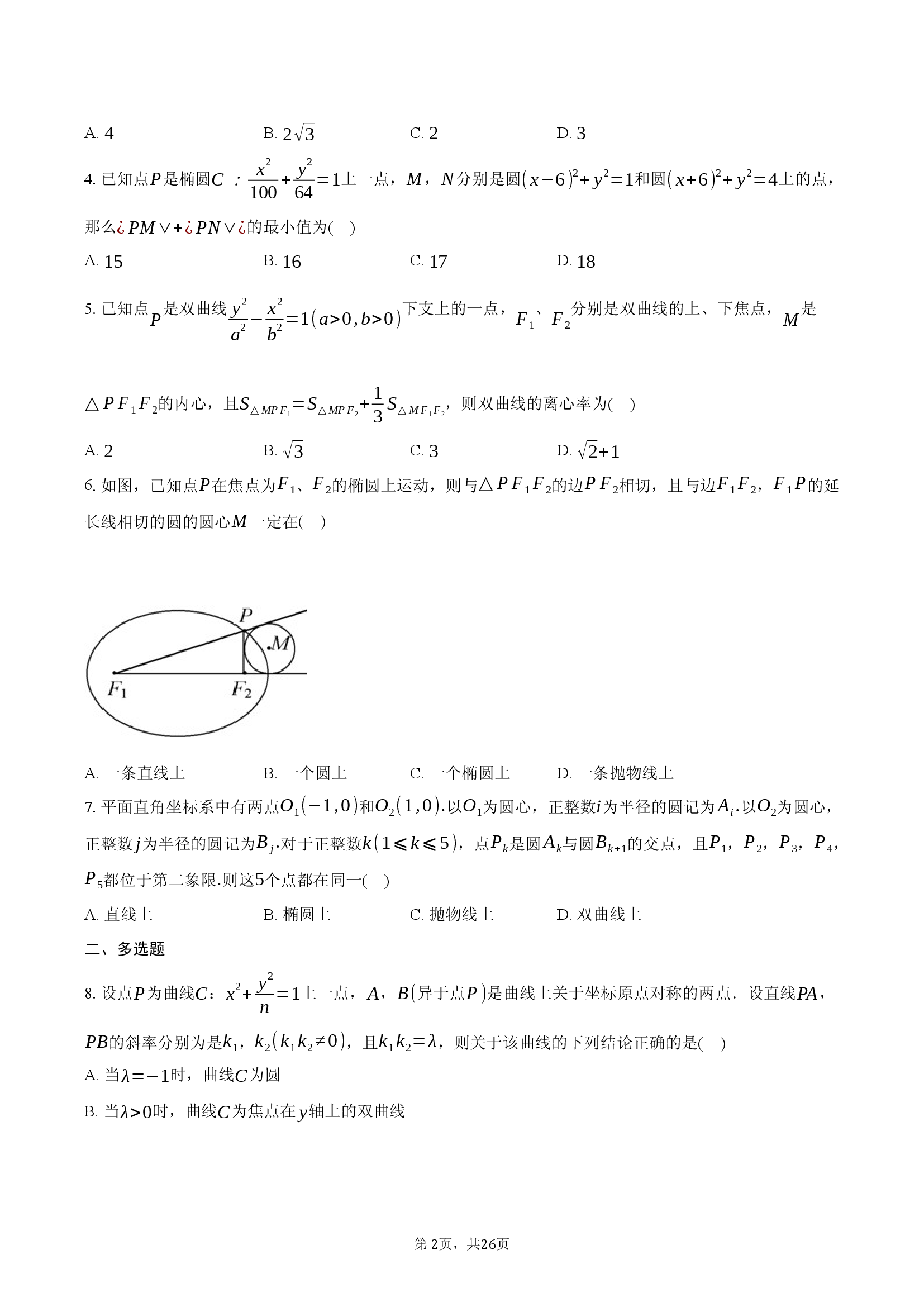
6
.
如图,已知点
在焦点为
、
的椭圆上运动,则与
的边
相切,且与边
,
的延长线相切的圆的圆心
一定在
( )
A.
一条直线上
B.
一个圆上
C.
一个椭圆上
D.
一条抛物线上
7
.
平面直角坐标系中有两点
和
以
为圆心,正整数
为半径的圆记为
以
为圆心,正整数
为半径的圆记为
对于正整数
,点
是圆
与圆
的交点,且
,
,
,
,
都位于第二象限
则这
个点都在同一
( )
A.
直线上
B.
椭圆上
C.
抛物线上
D.
双曲线上
二、多选题
8
.
设点
为曲线
:
上一点,
,
异于点
是曲线上关于坐标原点对称的两点.设直线
,
的斜率分别为是
,
,且
,则关于该曲线的下列结论正确的是
( )
A.
当
时,曲线
为圆
B.
当
时,曲线
为焦点在
轴上的双曲线
C.
当
时,曲线
为焦点在
轴上的椭圆
D.
当
时,曲线
为焦点在
轴上的椭圆
9
.
椭圆
:
的左右焦点分别为
,
为坐标原点,以下说法正确的是
( )
A.
过点
的直线与椭圆
交于
,
两点,则
的周长为
B.
椭圆
上存在点
,使得
C.
椭圆
的离心率为
D.
为椭圆
上一点,
为圆
上一点,则线段
的最大长度为
10
.
椭圆
:
的左右焦点分别为
,
,
为坐标原点,以下说法正确的是
( )
A.
过点
的直线与椭圆
交于
,
两点,则
的周长为
B.
椭圆
上存在点
,使得
C.
椭圆
的离心率为
D.
为椭圆
上一点,
为圆
上一点,则线段
的最大长度为
11
.
已知抛物线
,过焦点
的动直线
交抛物线于
,
两点,抛物线在
,
两点处的切线交于点
,则
( )
A.
点
在准线
上
B.
C.
,
,
三点的横坐标依次成等比数列
D.
三、解答题
12
.
已知双曲线
的焦点在坐标轴上,其渐近线方程为
,过点
.
求双曲线
的标准方程;
是否存在被点
平分的弦?如果存在,求出弦所在的直线方程;如果不存在,请说明理由.
13
.
已知直线
与抛物线
交于
,
两点,且线段
恰好被点
平分.
求直线
的方程;
抛物线上是否存在点
和
,使得
,
关于直线
对称?若存在,求出直线
的方程;若不存在,请说明理由.
14
.
设
,
分别是椭圆
的左、右焦点,
的离心率为
短轴长为
.
求椭圆
的方程:
过点
的直线
交椭圆
于
,
两点,是否存在实数
,使得
恒成立?若存在,求出
的值;若不存在,说明理由.
15
.
本小题
分
已知抛物线
:
的焦点为
,直线
:
与
交于
,
两点.
求
的方程.
求
的取值范围.
设点
,试问是否存在
,使得
?若存在,求
的值;若不存在,请说明理由.
16
.
已知椭圆
:
,点
、
分别是椭圆
的左焦点、左顶点,过点
的直线
不与
轴重合
交椭圆
于
,
两点.
求椭圆
的标准方程;
若
,求
的面积;
是否存在直线
,使得点
在以线段
为直径的圆上,若存在,求出直线
的方程;若不存在,请说明理由.
17
.
已知直线
与抛物线
交于
,
两点,且与
轴交于点
,过点
,
分别作直线
的垂线,垂足依次为
,
,动点
在
上
当
,且
为线段
的中点时,证明:
;
记直线
,
,
的斜率分别为
,
,
,是否存在
实数
,使得
?若...
2025年高三专项训练:圆锥曲线中的探究性问题.docx