第十章　§10.7　概率与统计的综合问题.docx

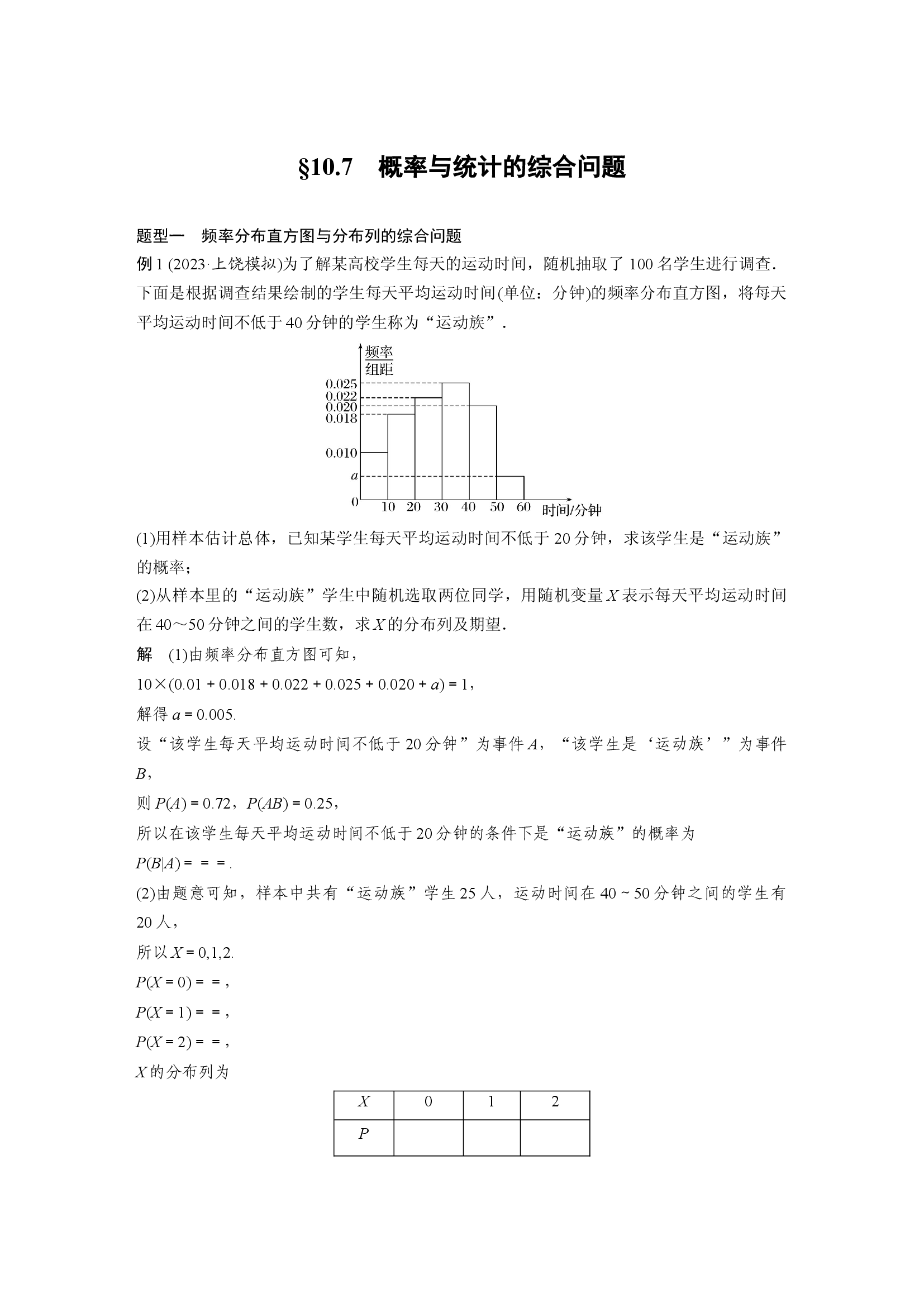
§10.7 　 概率与统计的综合问题 题型一　频率分布直方图与分布列的综合问题 例 1 ( 2023· 上饶模拟 ) 为了解某高校学生每天的运动时间 ， 随机抽取了 100 名学生进行调查 ． 下面是根据调查结果绘制的学生每天平均运动时间 ( 单位 ： 分钟 ) 的频率分布直方图 ， 将每天平均运动时间不低于 40 分钟的学生称为 “ 运动族 ” ． ( 1 ) 用样本估计总体 ， 已知某学生每天平均运动时间不低于 20 分钟 ， 求该学生是 “ 运动族 ” 的概率 ； ( 2 ) 从样本里的 “ 运动族 ” 学生中随机选取两位同学 ， 用随机变量 X 表示每天平均运动时间在 40 ～ 50 分钟之间的学生数 ， 求 X 的分布列及期望 ． 解 　 ( 1 ) 由频率分布直方图可知， 10 × ( 0.01 ＋ 0.018 ＋ 0.022 ＋ 0.025 ＋ 0.020 ＋ a ) ＝ 1 ， 解得 a ＝ 0.005. 设 “ 该学生每天平均运动时间不低于 20 分钟 ” 为事件 A ， “ 该学生是 ‘ 运动族 ’” 为事件 B ， 则 P ( A ) ＝ 0.72 ， P ( AB ) ＝ 0.25 ， 所以在该学生每天平均运动时间不低于 20 分钟的条件下是 “ 运动族 ” 的概率为 P ( B | A ) ＝ ＝ ＝ . ( 2 ) 由题意可知，样本中共有 “ 运动族 ” 学生 25 人，运动时间在 40 ～ 50 分钟之间的学生有 20 人， 所以 X ＝ 0 , 1 , 2. P ( X ＝ 0 ) ＝ ＝ ， P ( X ＝ 1 ) ＝ ＝ ， P ( X ＝ 2 ) ＝ ＝ ， X 的分布列为 X 0 1 2 P E ( X ) ＝ 0 × ＋ 1 × ＋ 2 × ＝ . 思维升华 高考常将频率分布直方图与分布列等交汇在一起进行考查，解题时要正确理解频率分布直方图，能利用频率分布直方图正确计算出各组数据 ． 概率问题以计算为主，往往和实际问题相结合，要注意理解实际问题的意义，使之和相应的概率计算对应起来 ． 跟踪训练 1 ( 2023· 呼和浩特模拟 ) 某高校共有 15 000 人 ， 其中男生 10 500 人 ， 女生 4 500 人 ， 为调查该校学生每周平均体育运动时间的情况 ， 采用按比例分配的分层随机抽样的方法 ， 收集 300 位学生每周平均体育运动时间的样本数据 ( 单位 ： 小时 ) ． ( 1 ) 应收集多少个女生样本数据 ？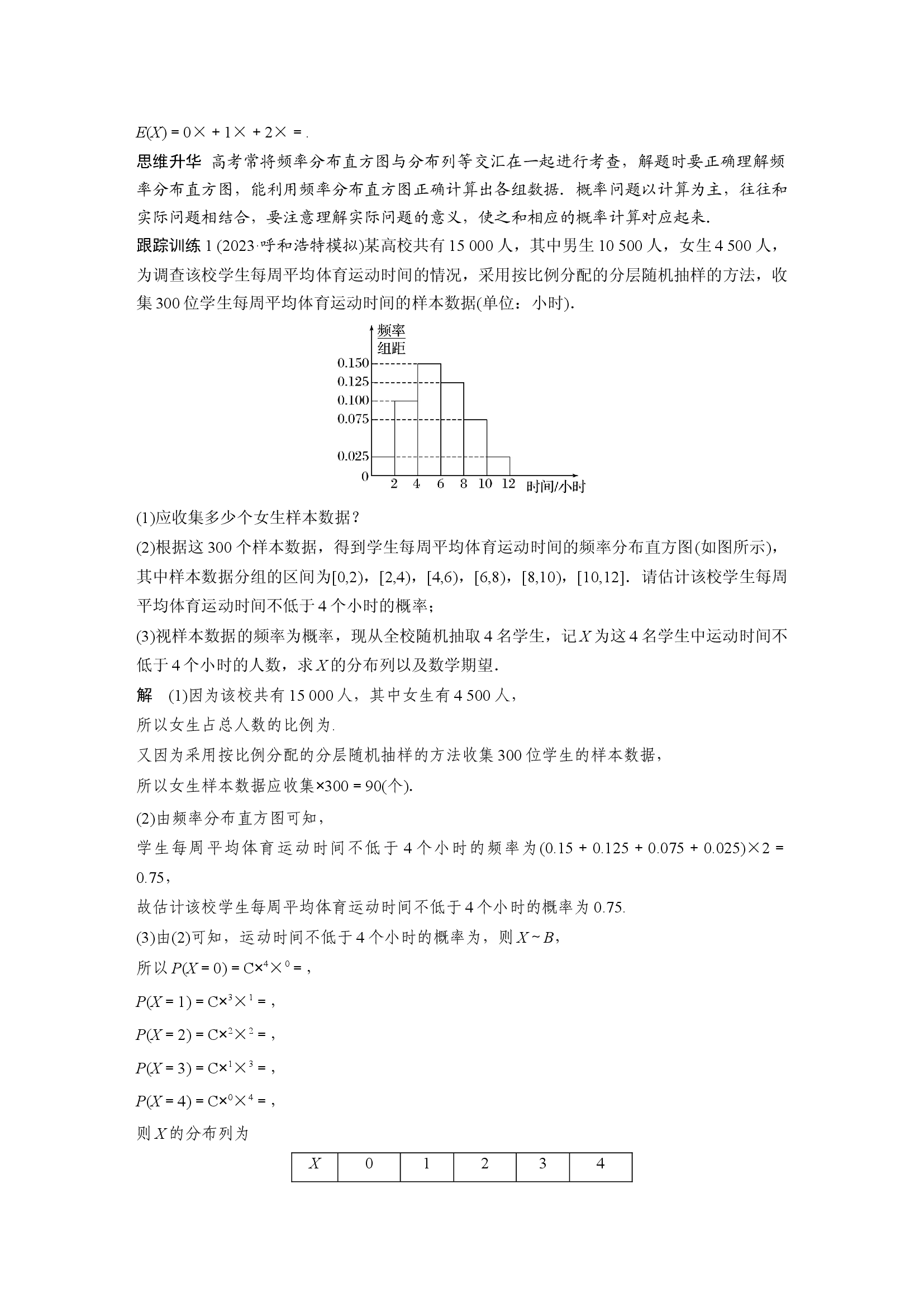 ( 2 ) 根据这 300 个样本数据 ， 得到学生每周平均体育运动时间的频率分布直方图 ( 如图所示 ) ， 其中样本数据分组的区间为 [ 0 , 2 ) ， [ 2 , 4 ) ， [ 4 , 6 ) ， [ 6 , 8 ) ， [ 8 , 10 ) ， [ 10 , 12 ] ． 请估计该校学生每周平均体育运动时间不低于 4 个小时的概率 ； ( 3 ) 视样本数据的频率为概率 ， 现从全校随机抽取 4 名学生 ， 记 X 为这 4 名学生中运动时间不低于 4 个小时的人数 ， 求 X 的分布列以及数学期望 ． 解 　 ( 1 ) 因为该校共有 15 000 人，其中女生有 4 500 人， 所以女生占总人数的比例为 . 又因为采用按比例分配的分层随机抽样的方法收集 300 位学生的样本数据， 所以女生样本数据应收集 × 300 ＝ 90 ( 个 ) ． ( 2 ) 由频率分布直方图可知， 学生每周平均体育运动时间不低于 4 个小时的频率为 ( 0.15 ＋ 0.125 ＋ 0.075 ＋ 0.025 ) × 2 ＝ 0.75 ， 故估计该校学生每周平均体育运动时间不低于 4 个小时的概率为 0.75. ( 3 ) 由 ( 2 ) 可知，运动时间不低于 4 个小时的概率为 ，则 X ～ B ， 所以 P ( X ＝ 0 ) ＝ C × 4 × 0 ＝ ， P ( X ＝ 1 ) ＝ C × 3 × 1 ＝ ， P ( X ＝ 2 ) ＝ C × 2 × 2 ＝ ， P ( X ＝ 3 ) ＝ C × 1 × 3 ＝ ， P ( X ＝ 4 ) ＝ C × 0 × 4 ＝ ， 则 X 的分布列为 X 0 1 2 3 4 P E ( X ) ＝ 4 × ＝ 3. 题型二　回归模型与分布列的综合问题 例 2 ( 2023· 韶关模拟 ) 研究表明 ， 如果温差大 ， 且人们不注意保暖 ， 可能会导致自身受到风寒刺激 ， 增加感冒患病概率 ， 特别是对于儿童以及年老体弱的人群 ， 要多加防范 ． 某中学数学建模社团成员研究了昼夜温差大小与某小学学生新增感冒就诊人数之间的关系 ， 他们记录了某六天的温差 ， 并到校医室查阅了这...