辽宁省协作体
2024-2025
学年高二上学期期末考试数学试卷
一
、
单选题(本大题共
8
个小题,每小题
5
分,共
40
分)
1.
已知随机变量
,若其对应的正
态密度函数
满足
,且
,则
(
)
A.
0.8
B.
0.5
C.
0.4
D.
0.1
【答案】
C
【解析】
由
,则正态密度函数
关于
对称,即
,
则
.
故选:
C.
2.
已知直线
的倾斜角为
,若
,则实数
的取值范围是(
)
A.
B.
C.
D.
【答案】
C
【解析】
因为
,所以
,即直线
的斜率
.
又由直线方程可得
,所以
,解得
,
即实数
的取值范围是
.
故选:
C.
3.
的展开式中,含
的项的系数为(
)
A
.
240
B.
C.
560
D.
360
【答案】
B
【解析】
的通项为
,
且
,
令
,解得
,故
的项的系数为
.
故选:
B.
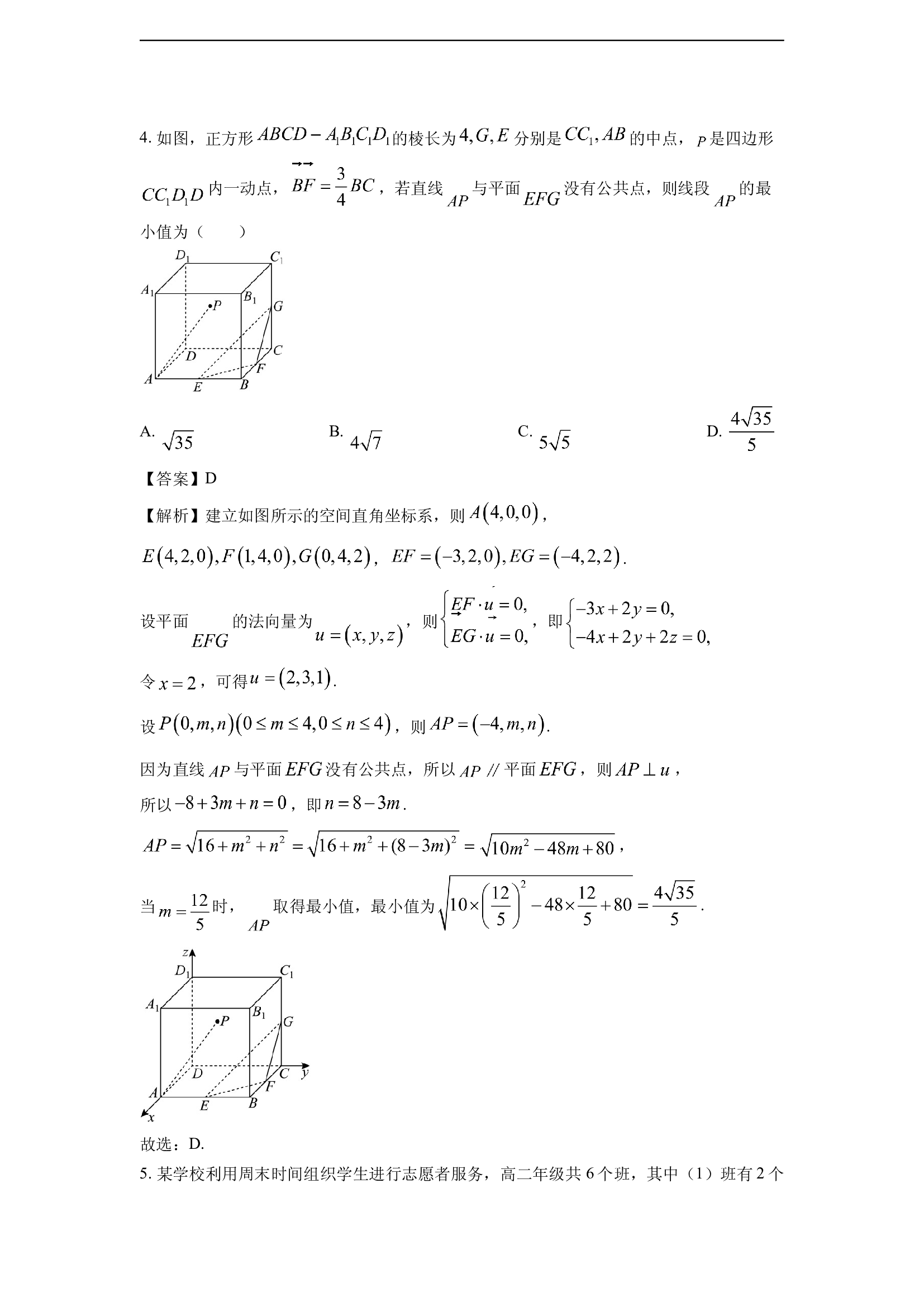
4.
如图,正方形
的棱长为
分别是
的中点,
是四边形
内一动点,
,若直线
与平面
没有公共点,则线段
的最小值为(
)
A.
B.
C.
D.
【答案】
D
【解析】
建立如图所示的空间直角坐标系,则
,
,
.
设平面
的法向量为
,
则
,即
令
,可得
.
设
,则
.
因为直线
与平面
没有公共点,所以
平面
,则
,
所以
,即
.
,
当
时,
取得最小值,最小值为
.
故选:
D
.
5.
某学校利用周末时间组织学生进行志愿者服务,高二年级共
6
个班,其中(
1
)班有
2
个志愿者队长,本次志愿者服务一共
20
个名额,志愿者队长必须参加且不占名额,若每个班
至少有
3
人参加,则共有(
)种分配方法
.
A.
90
B.
60
C.
126
D.
120
【答案】
C
【解析】
若每个班至少
3
人参加,由于(
1
)班有
2
个志愿者队长,
故只需先满足每个班级有
2
个名额,还剩
10
个名额,
再将
10
个名额分配到
6
个班级,每个班级至少
1
个名额,
故只需在
10
个名额中的
9
个空上放置
5
个隔板即可,有
种分配方法
.
故选:
C.
6.
已知菱形
的边长为
,以
为折痕把
折起,使点
到达点
的位置,且平面
平面
.
若点
都在同一球面上,则该球的表面积为(
)
A.
B.
C.
D.
【答案】
B
【解析】
如图所示,取
的中点
,连接
,
由题意可知
和
均为全等的等边三角形,
所以
,且
,
因为平面
平面
,平面
平面
,
所以
平面
,因为
平面
,所以
.
设
为球心,
为
的外心,
为
的外心,
则
平面
,
平面
,且
,
所以四边形
为正方形,即
.
又因为
的外接圆半径
,
所以在
中,
,即
,
所以球的表面积为
.
故选:
B.
7.
已知椭圆
的左,右焦点分别为
,点
是直线
上与点
不重合的动点,则
(数学试题试卷)辽宁省协作体2024-2025学年高二上学期期末考试试卷(解析版).docx